a k roy
Auteur:
debjit
Last Updated:
il y a 10 ans
License:
Creative Commons CC BY 4.0
Résumé:
quantum

\begin
Discover why over 25 million people worldwide trust Overleaf with their work.
quantum

\begin
Discover why over 25 million people worldwide trust Overleaf with their work.
\documentclass[preprint,floatfix] {revtex4}
\newcommand{\rvec}{\mathrm {\mathbf {r}}}
\usepackage{graphicx}
\usepackage{subfigure}
\usepackage{amsmath}
\usepackage{xcolor}
\usepackage{color, soul}
\begin{document}
\renewcommand{\thetable}{S\arabic{table}}
%%\begin{center}
%%\textbf{\large Supplemental Materials}
%%\end{center}
\begingroup
\squeezetable
\begin{table}
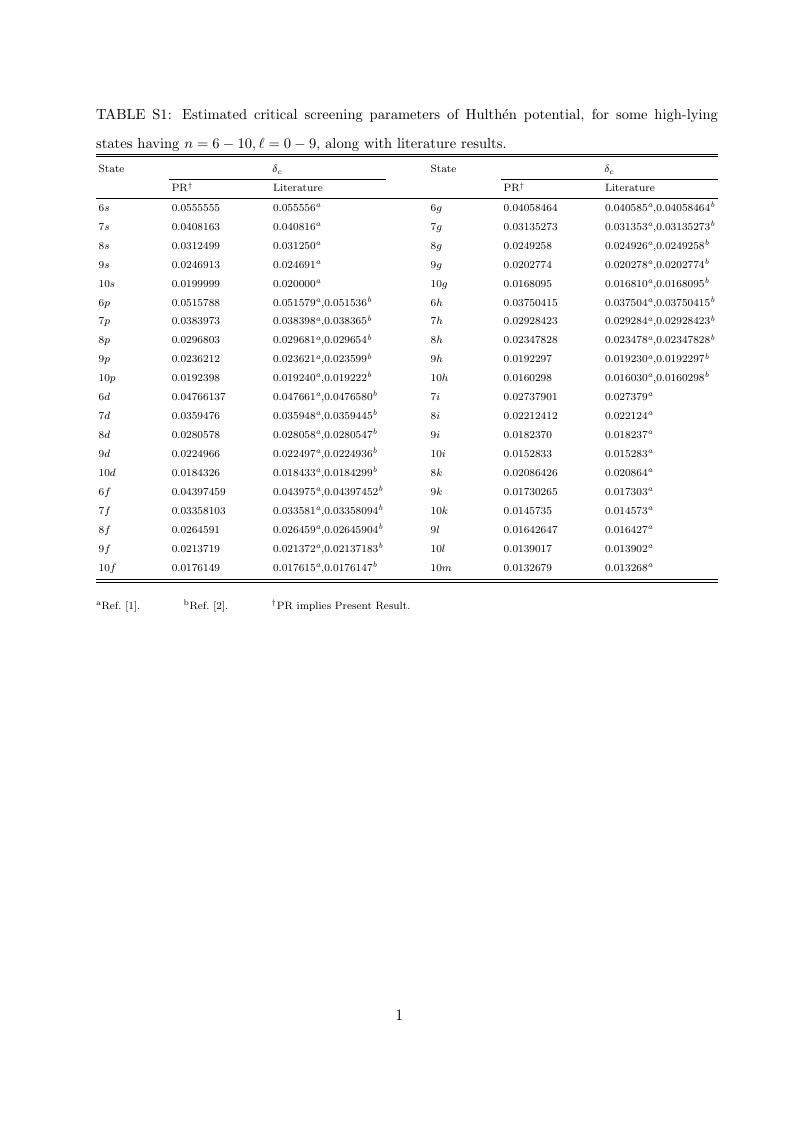
\caption {\label{tab:table1} Estimated critical screening parameters of Hulth\'en potential, for
some high-lying states having $n=6-10, \ell=0-9$, along with literature results.}
\begin{ruledtabular}
\begin{tabular}{llllll}
State & \multicolumn{2}{c}{$\delta_c$} & State & \multicolumn{2}{c}{$\delta_c$} \\
\cline{2-3} \cline{5-6}
& PR$^\dag$ & Literature &
& PR$^\dag$ & Literature \\ \hline
$6s$ & 0.0555555 & 0.055556\footnotemark[1] &
$6g$ & 0.04058464 & 0.040585\footnotemark[1],0.04058464\footnotemark[2] \\
$7s$ & 0.0408163 & 0.040816\footnotemark[1] &
$7g$ & 0.03135273 & 0.031353\footnotemark[1],0.03135273\footnotemark[2] \\
$8s$ & 0.0312499 & 0.031250\footnotemark[1] &
$8g$ & 0.0249258 & 0.024926\footnotemark[1],0.0249258\footnotemark[2] \\
$9s$ & 0.0246913 & 0.024691\footnotemark[1] &
$9g$ & 0.0202774 & 0.020278\footnotemark[1],0.0202774\footnotemark[2] \\
$10s$ & 0.0199999 & 0.020000\footnotemark[1] &
$10g$ & 0.0168095 & 0.016810\footnotemark[1],0.0168095\footnotemark[2] \\
$6p$ & 0.0515788 & 0.051579\footnotemark[1],0.051536\footnotemark[2] &
$6h$ & 0.03750415 & 0.037504\footnotemark[1],0.03750415\footnotemark[2] \\
$7p$ & 0.0383973 & 0.038398\footnotemark[1],0.038365\footnotemark[2] &
$7h$ & 0.02928423 & 0.029284\footnotemark[1],0.02928423\footnotemark[2] \\
$8p$ & 0.0296803 & 0.029681\footnotemark[1],0.029654\footnotemark[2] &
$8h$ & 0.02347828 & 0.023478\footnotemark[1],0.02347828\footnotemark[2] \\
$9p$ & 0.0236212 & 0.023621\footnotemark[1],0.023599\footnotemark[2] &
$9h$ & 0.0192297 & 0.019230\footnotemark[1],0.0192297\footnotemark[2] \\
$10p$ & 0.0192398 & 0.019240\footnotemark[1],0.019222\footnotemark[2] &
$10h$ & 0.0160298 & 0.016030\footnotemark[1],0.0160298\footnotemark[2] \\
$6d$ & 0.04766137 & 0.047661\footnotemark[1],0.0476580\footnotemark[2] &
$7i$ & 0.02737901 & 0.027379\footnotemark[1] \\
$7d$ & 0.0359476 & 0.035948\footnotemark[1],0.0359445\footnotemark[2] &
$8i$ & 0.02212412 & 0.022124\footnotemark[1] \\
$8d$ & 0.0280578 & 0.028058\footnotemark[1],0.0280547\footnotemark[2] &
$9i$ & 0.0182370 & 0.018237\footnotemark[1] \\
$9d$ & 0.0224966 & 0.022497\footnotemark[1],0.0224936\footnotemark[2] &
$10i$ & 0.0152833 & 0.015283\footnotemark[1] \\
$10d$ & 0.0184326 & 0.018433\footnotemark[1],0.0184299\footnotemark[2] &
$8k$ & 0.02086426 & 0.020864\footnotemark[1] \\
$6f$ & 0.04397459 & 0.043975\footnotemark[1],0.04397452\footnotemark[2] &
$9k$ & 0.01730265 & 0.017303\footnotemark[1] \\
$7f$ & 0.03358103 & 0.033581\footnotemark[1],0.03358094\footnotemark[2] &
$10k$ & 0.0145735 & 0.014573\footnotemark[1] \\
$8f$ & 0.0264591 & 0.026459\footnotemark[1],0.02645904\footnotemark[2] &
$9l$ & 0.01642647 & 0.016427\footnotemark[1] \\
$9f$ & 0.0213719 & 0.021372\footnotemark[1],0.02137183\footnotemark[2] &
$10l$ & 0.0139017 & 0.013902\footnotemark[1] \\
$10f$ & 0.0176149 & 0.017615\footnotemark[1],0.0176147\footnotemark[2] &
$10m$ & 0.0132679 & 0.013268\footnotemark[1] \\
\end{tabular}
\end{ruledtabular}
\begin{tabbing}
$^{\mathrm{a}}$Ref.~\cite{varshni90}. \hspace{25pt} \=
$^{\mathrm{b}}$Ref.~\cite{demiralp05}. \hspace{25pt} \=
$^\dag$PR implies Present Result.
\end{tabbing}
\end{table}
\endgroup
\begingroup
\squeezetable
\begin{table}
\caption {\label{tab:table2} Estimated critical screening parameters of Yukawa potential, for
some high-lying states having $n=6-10, \ell=0-9$, along with literature results. PR implies Present Result.}
\begin{ruledtabular}
\begin{tabular}{llllll}
State & \multicolumn{2}{c}{$\delta_c$} & State & \multicolumn{2}{c}{$\delta_c$} \\
\cline{2-3} \cline{5-6}
& PR & Literature~\cite{rogers70} &
& PR & Literature~\cite{rogers70} \\ \hline
$6s$ & 0.035182 & 0.03518 &
$6g$ & 0.023799103 & 0.02380 \\
$7s$ & 0.025874 & 0.0258 &
$7g$ & 0.018646215 & 0.01864 \\
$8s$ & 0.019824 & 0.0198 &
$8g$ & 0.014980862 & 0.01498 \\
$9s$ & 0.015672 & 0.0156 &
$9g$ & 0.012286145 & 0.01228 \\
$10s$ & 0.012699 & &
$10g$ & 0.010250170 & \\
$6p$ & 0.032174932 & 0.03217 &
$6h$ & 0.021524548 & 0.02152 \\
$7p$ & 0.024047639 & 0.0240 &
$7h$ & 0.017095135 & 0.01709 \\
$8p$ & 0.018640705 & 0.01864 &
$8h$ & 0.013883519 & 0.01388 \\
$9p$ & 0.014865869 & 0.01486 &
$9h$ & 0.011485753 & 0.01148 \\
$10p$ & 0.012128229 & &
$10h$ & 0.009651169 & \\
$6d$ & 0.029166650 & 0.02916 &
$7i$ & 0.015691083 & 0.01569 \\
$7d$ & 0.022161826 & 0.02216 &
$8i$ & 0.012871464 & 0.01287 \\
$8d$ & 0.017390648 & 0.01739 &
$9i$ & 0.010736147 & 0.01073 \\
$9d$ & 0.013999880 & 0.01400 &
$10i$ & 0.009082952 & \\
$10d$ & 0.011506513 & &
$8k$ & 0.011944531 & 0.01194 \\
$6f$ & 0.026350671 & 0.02635 &
$9k$ & 0.010039758 & 0.01003 \\
$7f$ & 0.020342170 & 0.02034 &
$10k$ & 0.008548707 & \\
$8f$ & 0.016156534 & 0.01615 &
$9l$ & 0.009395999 & 0.00939 \\
$9f$ & 0.013129670 & 0.01313 &
$10l$ & 0.008049285 & \\
$10f$ & 0.010872967 & &
$10m$ & 0.007584125 & \\
\end{tabular}
\end{ruledtabular}
\end{table}
\endgroup
\begingroup
\squeezetable
\begin{table}
\caption {\label{tab:table3} Estimated critical screening parameters of ECSC potential, for
some high-lying states having $n=6-10, \ell=0-9$, along with literature results. PR implies Present Result.}
\begin{ruledtabular}
\begin{tabular}{llllll}
State & \multicolumn{2}{c}{$\delta_c$} & State & \multicolumn{2}{c}{$\delta_c$} \\
\cline{2-3} \cline{5-6}
& PR$^\S$ & Literature &
& PR$^\S$ & Literature \\ \hline
$6s$ & 0.01787828 & 0.01787828\footnotemark[1],0.01787790\footnotemark[2] &
$6g$ & 0.0160994830 & 0.01609948\footnotemark[1],0.016099483\footnotemark[2] \\
$7s$ & 0.01312287 & 0.01312287\footnotemark[1],0.01312275\footnotemark[2] &
$7g$ & 0.0121108414 & 0.01211084\footnotemark[1],0.012110841\footnotemark[2] \\
$8s$ & 0.010041420 & 0.01004142\footnotemark[1],0.01004138\footnotemark[2] &
$8g$ & 0.0094255746 & 0.00942557\footnotemark[1],0.009425574\footnotemark[2] \\
$9s$ & 0.007930924 & &
$9g$ & 0.0075357713 & \\
$10s$ & 0.0064223221 & &
$10g$ & 0.0061576653 & \\
$6p$ & 0.0176520702 & 0.01765207\footnotemark[1],0.0176520692\footnotemark[2] &
$6h$ & 0.0154554769 & 0.01545548\footnotemark[1],0.015455476\footnotemark[2] \\
$7p$ & 0.0130010639 & 0.01300107\footnotemark[1],0.013001062\footnotemark[2] &
$7h$ & 0.0117204888 & 0.01172049\footnotemark[1],0.011720488\footnotemark[2] \\
$8p$ & 0.0099700872 & 0.00997009\footnotemark[1],0.009970085\footnotemark[2] &
$8h$ & 0.0091765721 & 0.00917657\footnotemark[1],0.009176572\footnotemark[2] \\
$9p$ & 0.0078864055 & &
$9h$ & 0.0073701634 & \\
$10p$ & 0.0063931148 & &
$10h$ & 0.0060436156 & \\
$6d$ & 0.0172429036 & 0.01724290\footnotemark[1],0.017242903\footnotemark[2] &
$7i$ & 0.0113144150 & 0.01131442\footnotemark[1],0.011314415\footnotemark[2] \\
$7d$ & 0.0127747014 & 0.01277470\footnotemark[1],0.012774701\footnotemark[2] &
$8i$ & 0.0089121305 & 0.00891213\footnotemark[1],0.008912130\footnotemark[2] \\
$8d$ & 0.0098352041 & 0.00983521\footnotemark[1],0.009835204\footnotemark[2] &
$9i$ & 0.0071912774 & \\
$9d$ & 0.0078012274 & &
$10i$ & 0.0059186845 & \\
$10d$ & 0.0063367620 & &
$8k$ & 0.0086398532 & 0.00863985\footnotemark[1],0.008639853\footnotemark[2] \\
$6f$ & 0.0167081500 & 0.01670815\footnotemark[1],0.016708150\footnotemark[2] &
$9k$ & 0.0070041846 & \\
$7f$ & 0.0124693824 & 0.01246938\footnotemark[1],0.012469382\footnotemark[2] &
$10k$ & 0.0057862828 & \\
$8f$ & 0.0096491922 & 0.00964919\footnotemark[1],0.009649192\footnotemark[2] &
$9l$ & 0.0068128353 & \\
$9f$ & 0.0076818589 & &
$10l$ & 0.0056491977 & \\
$10f$ & 0.0062568394 & &
$10m$ & 0.0055096394 & \\
\end{tabular}
\end{ruledtabular}
\begin{tabbing}
$^{\mathrm{a}}$Ref.~\cite{singh83}. \hspace{25pt} \=
$^{\mathrm{b}}$Ref.~\cite{nasser11}. \hspace{25pt} \=
\end{tabbing}
\end{table}
\endgroup
\begingroup
\squeezetable
\begin{table}
\caption {\label{tab:table4} Eigenvalues (a.u.) of $n=3,4$ states of confined ECSC potential for
$\delta=0.02$. Numbers in the parentheses denote reference energies quoted from \cite{lumb14}.}
\begin{ruledtabular}
\begin{tabular}{clllll}
State & $r_c=0.1$ & $r_c=0.5$ & $r_c=1$ & $r_c=2$ & $r_c=5$ \\
\hline
$3s$ & 4406.1416518 & 170.60516396 & 40.883123723 & 9.3341469004 & 1.0731978420 \\
& & & & (9.33415) & (1.07320) \\
$3p$ & 2960.4823022 & 114.66355228 & 27.493994384 & 6.2889991502 & 0.7276959975 \\
& & & & (6.28900) & (0.72770) \\
$3d$ & 1644.5499223 & 63.180184177 & 14.987462939 & 3.3475046681 & 0.3490909625 \\
& & & & (3.34750) & (0.34909) \\
$4s$ & 7857.6491849 & 308.21724725 & 75.150492179 & 17.836089963 & 2.4023028763 \\
& & & & (17.83609) & (2.40230) \\
$4p$ & 5918.2028888 & 232.44795983 & 56.778032985 & 13.530580567 & 1.8504011627 \\
& & & & (13.53058) & (1.85040) \\
$4d$ & 4115.6026320 & 161.37700634 & 39.335318864 & 9.3341465110 & 1.2596272053 \\
& & & & (9.33415) & (1.25963) \\
$4f$ & 2426.4155489 & 94.646597432 & 22.915824203 & 5.3620893411 & 0.6894218988 \\
& & & & (5.36209) & (0.68942) \\
\hline
& $r_c=10$ & $r_c=20$ & $r_c=30$ & $r_c=50$ & $r_c=100$ \\
\hline
$3s$ & 0.1113277900 & $-$0.0302492345 & $-$0.0358787689 & $-$0.0360250925 & $-$0.0360251051 \\
& (0.11133) & & & ($-$0.03603) & \\
$3p$ & 0.0691008416 & $-$0.0319140038 & $-$0.0358733580 & $-$0.0359675961 & $-$0.0359676034 \\
& (0.06910) & & & ($-$0.03597) & \\
$3d$ & 0.0128160637 & $-$0.0342064512 & $-$0.0358194164 & $-$0.0358506603 & $-$0.0358506623 \\
& (0.01282) & & & ($-$0.03585) & \\
$4s$ & 0.4250635505 & 0.0363462881 & $-$0.0054277289 & $-$0.0124953824 & $-$0.0125717772 \\
& (0.42506) & & & ($-$0.01250) & \\
$4p$ & 0.3359680167 & 0.0277302857 & $-$0.0066764629 & $-$0.0124281276 & $-$0.0124857523 \\
& (0.33597) & & & ($-$0.01243) & \\
$4d$ & 0.2223514916 & 0.0141166051 & $-$0.0086778605 & $-$0.0122798641 & $-$0.0123102664 \\
& (0.22235) & & & ($-$0.01228) & \\
$4f$ & 0.1081309850 & $-$0.0003604550 & $-$0.0106312256 & $-$0.0120295162 & $-$0.0120381878 \\
& (0.10813) & & & ($-$0.01203) & \\
\end{tabular}
\end{ruledtabular}
\end{table}
\endgroup
\clearpage
\begin{thebibliography}{99}
\bibitem{varshni90} Y.~P.~Varshni, Phys.~Rev.~A \textbf{41}, 4682 (1990).
\bibitem{demiralp05} M.~Demiralp, Appl.~Math.~Comput.~ \textbf{168}, 1380 (2005).
\bibitem{rogers70} F.~J.~Rogers, H.~C.~Graboske Jr.~ and D.~J.~Harwood, Phys.~Rev.~A \textbf{1}, 1577 (1970).
\bibitem{gomes94} O.~A.~Gomes, H.~Chacham and J.~R.~Mohallem, Phys.~Rev.~A \textbf{50}, 228 (1994).
\bibitem{lam72} C.~S.~Lam and Y.~P.~Varshni, Phys.~Rev.~A \textbf{6}, 1391 (1972).
\bibitem{ray80} P.~P.~Ray and A.~Ray, Phys.~Lett.~ \textbf{78A}, 443 (1980).
\bibitem{singh83} D.~S.~Singh and Y.~P.~Varshni, Phys.~Rev.~A \textbf{28}, 2606 (1983).
\bibitem{nasser11} I.~Nasser, M.~S.~Abdelmonem and A.~Abdel-Hady, Phys.~Scr.~ \textbf{84}, 045001 (2011).
\bibitem{lumb14} S.~Lumb, S.~Lumb and V.~Prasad, Phys.~Rev.~A \textbf{92}, 032505 (2014).
\end{thebibliography}
\end{document}