overleaf template galleryLaTeX templates and examples — Recent
Discover LaTeX templates and examples to help with everything from writing a journal article to using a specific LaTeX package.

"ModernCV" CV and Cover Letter LaTeX Template Version 1.1 (9/12/12) This template has been downloaded from: http://www.LaTeXTemplates.com Original author: Xavier Danaux (xdanaux@gmail.com) License: CC BY-NC-SA 3.0 (http://creativecommons.org/licenses/by-nc-sa/3.0/)

This template does not comply with the design manual at the University of Oslo from 2022. Beamer theme for the Department of Mathematics at the University of Oslo. Documentation: https://github.com/martinhelso/MathDept

Template do relatório de física experimental da UFC.
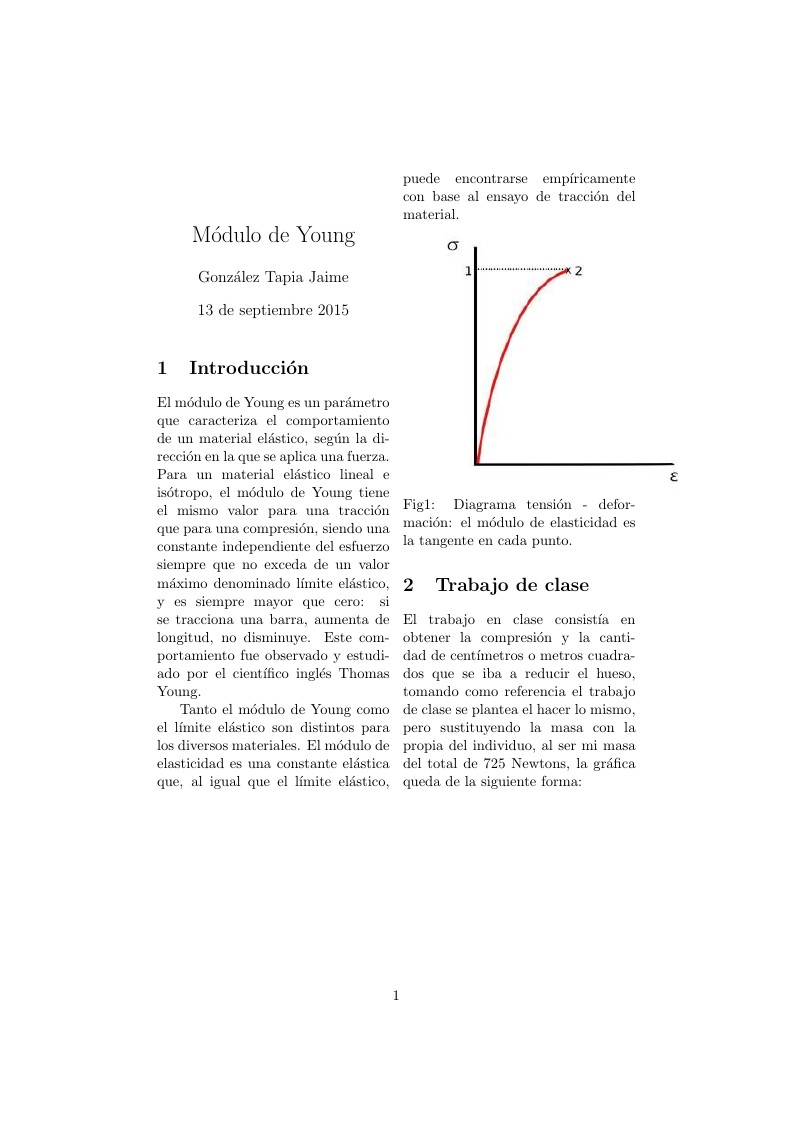
trabajo universitario con explicación breve del módulo de young

Unfinished review of precal

Simpel skabelon/template/preamble til foredraget "LaTeX for Begyndere" for Mat/Fys Studenterråd ved Aarhus Universitet (Februar 2019).

With Overleaf, edit online instantly this Conference Poster (NIWeek 2014), and download a PDF version. This project is also available on my web site

Original author: Rahul Chauhan Original repository: https://rahulworld.github.io
![Modelo de Trabalho Acadêmico [Udesc]](https://writelatex.s3.amazonaws.com/published_ver/39942.jpeg?X-Amz-Expires=14400&X-Amz-Date=20260113T061829Z&X-Amz-Algorithm=AWS4-HMAC-SHA256&X-Amz-Credential=AKIAWJBOALPNFPV7PVH5/20260113/us-east-1/s3/aws4_request&X-Amz-SignedHeaders=host&X-Amz-Signature=42f6ee4fe80df8361b2d789b8cfed4df753eb6dd72d19fe679c24ca6772b158d)
Este template é um personalização para a universidade UDESC com base nos arquivos do grupo abnTeX2. Este modelo está em constante desenvolvimento e sua utilização é de inteira responsabilidade do usuário.
\begin
Discover why over 20 million people worldwide trust Overleaf with their work.